Espacio Logopedico
Las matemáticas aplicadas en el arte
En general, cuando se construye conocimiento matemático, hay momentos en los que es importante detenerse a observar lo que se ha hecho, quizás, esa observación concluye en la determinación de alguna regularidad, útil para hacer la construcción del pensamiento. El artículo tiene como objetivo ilustrar la aplicación de la sección áurea en al arte y ver la aplicación de las matemáticas en forma práctica, útil y divertida.
Introducción
“…solamente en aprender definiciones y teoremas, para reconocer el momento de utilizarlos y aplicarlos… hacer matemáticas implica ocuparse de problemas. Sólo se hacen matemáticas cuando nos ocupamos de problemas, pero se olvida que resolver un problema es parte del trabajo; encontrar buenas preguntas es tan importante como encontrar soluciones. Una buena reproducción por el estudiante de actividad científica exigiría que intervenga, que formule, que pruebe, que construya modelos, lenguajes, conceptos, teorías, que intercambie con otros, que reconozca los que están conformes con la cultura, que tome lo que es útil,…Por supuesto, se trata de una simulación que no es la “verdadera” actividad científica, como tampoco el saber presentado de forma axiomática constituye el “verdadero saber” (Brousseau, 1986).
Los programas de Matemáticas de la Escuela Nacional Preparatoria, que imparten la materia obligatoria y con carácter teórica, muestra cambios significativos en la estructura, secuencia de los contenidos y en su enfoque metodológico, basado en la solución de problemas y no en relación aplicaciones prácticas.
Por medio de los contenidos propuestos, pretende que el alumno conozca, comprenda y aplique el aprendizaje de una forma tradicional como lo marca la etapa de la educación de tecnología de la educación y no el constructivismo que marca las propuestas institucionales.
Metodología
Método: Un rectángulo especial es el llamado rectángulo áureo. Se trata de un rectángulo armonioso en sus dimensiones (Caro, 1936).
Dibujamos un cuadrado y marcamos el punto medio de uno de sus lados. Lo unimos con uno de los vértices del lado opuesto y llevamos esa distancia sobre el lado inicial, de esta manera obtenemos el lado mayor del rectángulo.
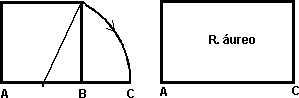
Si el lado del cuadrado vale 2 unidades, es claro que el lado mayor del rectángulo vale 1+ v5 por lo que la proporción entre los dos lados es:(1+ v5 ) /2
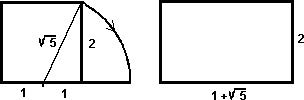
A este número se le llama número de oro, se representa por el símbolo Ø y su valor es 1,61803..., lo obtuvieron los griegos al hallar la relación entre la diagonal de un pentágono y el lado. El nombre de "número de oro" se debe a Leonardo da Vinci.
G R A T I S
Imprimir
Tamaño original
Ampliar texto
Reducir texto
-
Conjunto de ropa de entretiempo vaquero, falda con bonitas flores y cinta naranja para muñeco/a bebé de 21 cm. Presentado en bolsa...7.80 € -
Esta obra forma parte del conjunto de volúmenes que dedicamos a la orientación de los opositores de Psicología y Pedagogía....24.00 € -
En ¿Dónde está el señor Unicornio?, los pequeños lectores deben encontrar la sirena, el dragón, el hada y el unicornio. Cuando lev...8.95 € -
Este volumen desarrolla los temas 1 a 18 del temario de Matemáticas para el acceso al cuerpo de Profesores de Enseñanza Secundaria...45.00 €
ARTÍCULOS RELACIONADOS
- Sentirse en la Escuela como en Casa….
- Los títeres en arteterapia. (Parte I)
- Musicoterapia en la tercera edad. (Parte I)
- Comentarios sobre mi trabajo como Docente de Música en la Escuela Primaria. (Parte III)
- Los títeres en arteterapia. (Parte I)
- Musicoterapia en la tercera edad. (Parte I)
- Comentarios sobre mi trabajo como Docente de Música en la Escuela Primaria. (Parte III)
- Arteterapia: la sana-acción de crear. (Parte I)
- Matemáticas con regletas de Cuisenaire
