3.    Resolución de problemas

Actualmente, desde el currículo está presente el propósito de aprender matemáticas a través de la resolución de problemas; sin embargo, para cumplirlo resulta imprescindible considera desde ¿qué es un problema aritmético? ¿qué tipos de problemas existen? Y de ellos ¿cuáles plantear a los alumnos?

En el presente apartado, se busca dar respuesta a las preguntas anteriores al dar un panorama general acerca de esta temática.

Para explicar los tipos de problemas aditivos utilizados en este estudio procederemos de la siguiente forma: se explican primeramente las clases de problemas aditivos de acuerdo con su estructura verbal, su categoría semántica y sus relaciones. Estas clases tienen que ver con características muy particulares inherentes a ellos. Como son: las acciones y relaciones dentro del problema, las palabras utilizadas en el texto, las características semánticas y el tipo de relación implicada en el problema. Sin embargo, para nuestro estudio se establece una nueva clasificación que, si bien, puede incluir a las anteriores, no abarca las singularidades que acabamos de mencionar, como se observa en la figura 3.1.

 

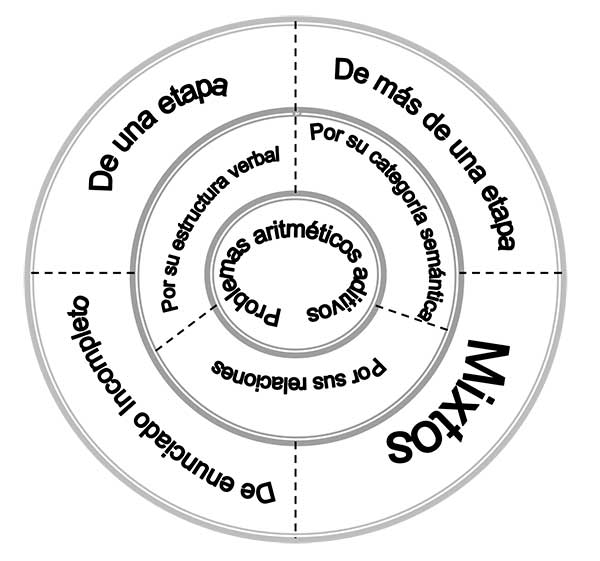
Fig. 3.1 Clasificación de problemas aditivos

 

Es por ello que el apartado concerniente al tratamiento de los tipos de problemas utilizados se ha titulado “Hacia una clasificación de problemas aditivos”; y de acuerdo a ésta se catalogan los utilizados en la presente investigación.

3.1  ¿Qué es un problema?

 

Los problemas que se utilizan en la escuela se presentan en enunciados para ser resueltos por los alumnos, para entenderlos describiremos las características de su enunciado y su resolución.

En el enunciado, los datos se presentan con la cantidad expresando las relaciones entre ellas y la pregunta pide determinar una o varias cantidades; su resolución consiste en realizar una o varias operaciones (Puig y Cerdán, 1988).

Un problema puede considerarse aritmético siempre que los conceptos o recursos no estrictamente aritméticos del contexto que aparecen en el enunciado no sean decisivos al resolverlo. De los problemas aritméticos este estudio se abocará a los aditivos (suma y resta) y dejamos de lado los de multiplicación y división.

Una distintiva más de los problemas escolares es que, además de ser resueltos por los alumnos, no se proponen únicamente con ese fin; su intención va más adelante al utilizarlo como medio de aprendizaje y/o evaluación (Puig y Cerdán, 1988).

 

 

3.2 Clasificación de los problemas aritméticos verbales

 

En este apartado, se mencionan algunas de las clasificaciones de problemas verbales encontradas en la literatura de investigación.

Consideremos importante aclarar el hecho de que se han nombrado genéricamente ‘problemas aritméticos verbales’ aún cuando algunos autores   los manejan como ‘problemas verbales’ y otros como ‘problemas aritméticos’ al referirse a los tipos que son utilizables en la escuela primaria.

Las clasificaciones aquí mencionadas nos dan un panorama general de diversas tipologías de problemas de problemas y coadyuvan a delimitar los tipos utilizados en este estudio.

a) Por las características de estructura verbal

 

En esta clasificación se distinguen seis clases diferentes de problemas aditivos en tres dimensiones caracterizadas por las acciones y relaciones involucradas en los problemas. La primera se refiere a distinguir entre una relación estática o activa entre los  conjuntos  de  objetos  implicados  en  el  problema;  la  segunda,  involucra  una

 

inclusión  de  conjuntos  o  una  interrelación  conjunta-subconjunto;  y  la  tercera, involucra acción que aumenta o disminuye la cantidad dada (Carpenter y Monser,1982).

Los seis diferentes tipos de problemas aditivos basados en estas dimensiones son:

 

-Reunión. Involucra acción en un proceso de poner activamente juntas dos cantidades. La cantidad inicial se opera directamente originando su aumento o disminución.

-Separación. Sus características son similares al anterior, se distinguen porque un subconjunto es removido del conjunto dado.

-Parte-parte-todo. Describen una relación estática entre una cantidad y sus dos partes. Comparación. Implica comparar dos cantidades disjuntas. Buscar la diferencia entre dos cantidades o dada una cantidad y su diferencia con otra, se busca la segunda cantidad.

-Igualación-aumentado e Igualación-quitando. Se distinguen por la interrelación conjunta – sub-conjunto que implican. Involucran el mismo tipo de acciones de los problemas de reunión y separación. Igualar-aumentando implica un aumento de la cantidad más pequeña, mientras que en igualar-quitando hay una disminución de la cantidad más grande.

Para cada clase de problemas aditivos hay tres distintas variables referentes a la naturaleza de la incógnita sobre las que no se ahondará aquí por no tener relevancia para este estudio.

b) Por su categoría semántica

 

El contenido verbal de los problemas aritméticos aditivos ha sido estudiado en dos sentidos, por un lado, existe un análisis fragmentado de las palabras utilizadas en el texto del problema y por otro, un análisis global atendiendo el sentido del texto como un todo.

Nesher (1982), resume la dependencia semántica dada por siete tipos de palabras:

-Argumentos. Dependencia semántica entre los argumentos cuantificados de manera numérica que tiene lugar en los lazos que subyacen al texto del problema.

-Adjetivos. Los adjetivos califican a los argumentos cuantificados.

 

-Agentes. Dependencia semántica debido a los agentes a quienes se refiere el texto.

 

-Ubicación. Dependencia semántica debido a la relación espacial de los objetos.

 

-Tiempo. Dependencia semántica debido a la relación temporal entre los momentos a que se refiere el texto.

-Veros. Dependencia semántica expresada en términos de verbos que se encuentran en el texto.

-Tiempos   relacionales.   Dependencia  semántica  debido   a  términos   relacionales respecto a dos argumentos dados.

Considerando  el  significado  global  del  texto  del  problema  aditivo,  existe  una clasificación desde un punto de vista semántico en cuatro categorías (Puig y Cerdán,

1988):

 

-Cambio. Las relaciones lógicas aditivas están contenidas en una secuencia temporal de sucesos. S distinguen tres momentos diferentes en los que se describe cómo la cantidad inicial es sometida a una acción directa o sobreentendida que la modificada.

-Combinación. La pregunta de problemas trata acerca del todo o de una de las partes, con lo que hay dos tipos posibles de problemas de combinar, los que se resuelven con una suma y los que se llega a la respuesta por una resta.

-Comparación. Las cantidades presentes en el problema se denominan cantidades de referencia, cantidad compara y diferencia. El sentido de la comparación puede establecer en más o menos y se puede preguntar por las tres cantidades.

-Igualación. Hay una comparación entre las cantidades que aparecen, establecida por medio del comparativo de igualdad ‘tantos como’.

 

 

 

c) Por sus relaciones

 

Al considerar la resolución de problemas aditivos como un recurso base del conocimiento operacional,  se una clasificación que abarque la mayoría de los tipos de problemas agrupándolos en seis tipos principales de relaciones.

-Composición de dos medidas.

 

-Una transformación une dos medidas. Estado-transformación-estado.

 

-Una relación estática une dos medidas. Estado-relación-estado.

 

-Composición       de       dos       transformaciones.       Transformación-transformació- transformación.

-Una transformación une dos relaciones estáticas. Relación-transformación-relación.

 

-Composición de dos relaciones estáticas. Relación-relación-relación.

 

Esta  clasificación  depende  de  la  distinción  entre  tres  conceptos  principales:

 

medida, transformación de tiempo y relación estática.

 

 

 

3.3  Hacia una clasificación de problemas aritméticos

 

Una Vez recorridas algunas clasificaciones para los problemas aritméticos verbales se hará mención de los tipos utilizados para este estudio, es importante aclarar que se toman  de  las  categorías  enunciadas  por  los  autores  que  contribuyen  al  logro  de nuestros propios propósitos.

Por este motivo, se enuncian a continuación los siguientes tipos de problemas:

 

a) Problema aritmético elemental verbal de una etapa

 

En una clasificación establecida por Puig y Cerdán (1988) Problema aritmético elemental de una etapa, se le ha dado el nombre mencionado por ser mas acorde a este estudio; un rasgo fundamental de este tipo de problemas es encontrar una cantidad a partir de otras que se proporcionan y, por lo tanto, son conocidas.

Se distinguen dos partes: información y pregunta; independientemente de que por la estructura sintáctica del problema sean separables más o menos fácilmente. Siempre existen dos datos, dejando de lado los no pertinentes o redundantes que puedan aparecer.

Las palabras contenidas pueden o no desempeñar algún papel en la operación, en este caso sólo sirve para conectar el problema a la realidad o ubicarlo en una situación concreta determinada.

Sin embargo, siempre existen palabras clave que puedan ser propias de la terminología matemática (añadir, sustraer, dividir, etc.), palabras conectivas cuya significación en el texto coadyuva a la elección de la operación precisada para llegar a la solución y palabras que expresan relaciones.

b)  Problema  aritmético  elemental  verbal  de  más  de  una  etapa  o  de  varias operaciones

 

Puig y Cerdán (1988) diferencian este tipo de problemas de los anteriores porque siempre hay más de dos datos y las relaciones entre ellos y la incógnita son más complejas aunque esto se deba sólo al hecho del aumento en los datos. Por lo tanto, los cálculos por realizar para obtener la respuesta no es una expresión aritmética

simple.

 

Este tipo de problemas requiere tomar tres decisiones: qué operaciones entre qué cantidades y en cuál orden.

Llegar a su solución requiere construir enunciados de problemas de una etapa mediante incógnitas que no están explícitamente en el texto del problema.

c) Problemas con enunciado incompleto

 

Proponemos  esta  clase  de  problemas  considerando  las  siguientes características:

Son problemas no rutinarios en la enseñanza que permiten estimular una resolución más cuidadosa y un punto de vista más realista de la resolución genuina de problemas (Baroody, 1988).

Las finalidades en su uso pueden ser: dada la incógnita se piden los datos del problema (Puig y Cerdán, 1988), analizar los datos y separar la información necesaria de la innecesaria, hacer caso omiso de la información extra (Baroody, 1988).

d) Problemas mixto

 

Estos se distinguen porque parte de la información se encuentra en una ilustración de la cual se hacen las interrogantes a resolver por los alumnos.

Los cuatro tipos de problemas abordados en este apartado son los tipos que han contribuido con los propósitos de este estudio, por este motivo se señalan de manera particular.

 

 

3.4 Implicaciones y estrategias de resolución de problemas

El conocimiento que tiene verdadera significación es el que forja el alumno, en este sentido, la resolución de problemas es el lugar de la producción de conocimiento. Así, el proceso de resolución debe llevar a lo anterior.

a) Implicaciones de resolver problemas

 

A continuación se abordarán las implicaciones de la resolución de problemas propuestas a través de las fases de la resolución y cómo ir superando cada una.

Estas  implicaciones  se  considerarán  en  este  estudio  en  las  sesiones  de enseñanza al abordar en ellas los diversos tipos de problemas, para observar si los alumnos las recorren en sus propios procesos de resolución y tener lineamientos para el análisis de esta parte del estudio.

-Comprensión del problema. Ver claramente qué se pide. Diferenciar los datos, observar si la condición es suficiente para encontrar la incógnita del estudio.

-Concebir un plan. Saber al menos a ‘grosso modo’ qué cálculos pueden llevar a determinar la incógnita. Para ello son necesarias una serie de circunstancias, conocimientos ya adquiridos, buenos hábitos de pensamiento y concentración.

-Ejecución del plan. Una vez el plan lo que procede es ejecutarlo, examinando los detales parcialmente hasta todo esté perfectamente claro.

-Examinar la solución obtenida. Para esto, se vuelve atrás en el problema para revisar y discutir tanto el resultado como el procedimiento que los levó a él.

Las aportaciones teóricas  nos permiten tener elementos para abordar el análisis de cómo resolvieron los niños los problemas aditivos durante las sesiones de enseñanza.

b) Estrategias de resolución

 

Las estrategias de resolución de problemas identificadas por Carpenter y Monser (1982), en niños de primer grado, corresponden a tres niveles básicos: a través de un medelo directo con objetos físicos o dedos, basadas en el uso de conteo de series y por evocación de hechos numéricos. Estas estrategias se mencionan a continuación:

-“Contar todos”. Consiste en contar el conjunto resultante comenzando desde el uno, después de haber representado las cantidades con objetos o dedos.

-“Contar hacia arriba desde el primero y contar hacia arriba desde el mayor”. Estas dos estrategias se utilizaran sin la mediación de objetos físicos, consiste en comenzar el recuento a partir de uno de los números dados; a partir del primer número que aparezca en el problema o desde el mayor.

-“Quitar de” y “quitar hasta”. Se realiza con modelos físicos y consiste en separar del total una parte. En “quitar de” se separa la otra cantidad y se obtiene la solución por recuento de lo que queda. En “quitar hasta” se separa del total lo que hace falta separar para tener la otra cantidad y se obtiene la solución por recuento de lo que se ha dado.

-“Contar hacia abajo desde” y “contar hacia abajo hasta”. Corresponden con las anteriores y se diferencian por no requerir de ningún modelo físico.

-“Añadir hasta” y “contar hacia arriba desde”. Son estrategias de problemas de sustracción que invocan acciones aditivas. La primera se realiza en un modelo físico y la segunda directamente  sobre las  cantidades.  Ambas  consisten  desde  la cantidad mayor hasta la menor.

-“Emparejar”. Consiste en el apareamiento sobre un modelo físico de las cantidades y el recuento posterior de la parte que queda.

Estas estrategias coadyuvan al análisis de las respuestas de los sujetos de nuestro estudio, dadas a los problemas aditivos planteados.

 

 

3.5 Enseñanza basada en la resolución de problemas

En la enseñanza tradicional, el uso de problemas aritméticos verbales suele realizarse después de introducir una operación con fines como dominar los datos numéricos de dicha operación, practicar los algoritmos y reforzar aplicaciones específicas de las operaciones. De esta manera, la utilización de los problemas se limita a practicar técnicas básicas, no a desarrollar la capacidad de resolverlos (Baroody, 1988).

Con la clasificación presentada para este estudio, una implicación directa a la enseñanza directa a la enseñanza se refiere a plantearlos antes del dominio de técnicas básicas, con el propósito de crear un puente importante entre los conceptos y procedimientos informales de los alumnos.

Aún cuando se comienza con problemas que simplemente consiste en realizar cálculos para llegar a una respuesta, presentar problemas no rutinarios permiten a los alumnos separar la información útil de la irrelevante (Baroody, 1988).

Uno  de los  objetivos  de  la  enseñanza  mediante  resolución  de  problemas consiste en distinguir entre:

…Lo razonable y lo absurdo, lo lógico y lo ilógico, entonces hay razones para plantearse el uso de todos los tipos de problemas

 

(Puig y Cerdán, 1988, p.199).

 

La enseñanza debe proporcionar a los alumnos la oportunidad de discutir los problemas y expresar sus dudas, además de ser empleados como medio de discutir los problemas y expresar sus dudas, además de ser empleados como medio de desarrollar el hábito de leer el texto significativamente y críticamente, así, contribuir a la comprensión de un problema aritmético verbal en todas sus partes (Puig y Cerdán,

1988).

 

 

 

4.    Concepto de número y problema

 

A lo largo de este escrito se ha recurrido en torno al número y problema de manera separada, sin embargo, considero que existe una gran relación entre ambas.

Para el primer argumento consideremos a Piaget. Se ha mencionado que uno de los métodos utilizados por él fue el de resolución de problemas (Piaget e Inheler,

1978a). Si bien es evidente que no se presentaron como problemas verbales, esto nos da  un  primer  indicio  de  interrelación  entre  construcción  del  número  natural  y resolución de problemas aditivos.

Posteriormente,  se  hizo  referencia  al  conteo  tanto  en  la  construcción  del número como en las estrategias de resolución de problemas, por este motivo tenemos nuevamente un punto de coincidencia entre ambas temáticas.

Finalmente, se ha explicado que la resolución de problemas puede tener diversos objetivos. Superar el uso que se les ha dado en la enseñanza tradicional implica entender las matemáticas como una forma de pensar que conciba la resolución de los problemas como el objetivo fundamental de la enseñanza y como medio de enseñar los conceptos matemáticos (Resnick y Ford, 1990).

 

Referencias

Baroody, A.J. (1988). El pensamiento matemático de los niños. Madrid.

Carpenter, T. y Monser, J.(1982). The Development of Addition and Subtraction Problem. Sonving Skill.

Fuson, K.C. y Hall, J.W. (1983). The developtment of mathematical thinking. Academic Press

Inc. Chapter 2.

Fuson, K.C.(1988). Children´s counting and concepts of number. New York. Kamii, C. (1984). El número en la educación preescolar. Madrid.

Nesher, P.(1982). Levels of Description in the Analysis of Addition and Sustraction Word

Problems. Lawrence Erlbaum Associates, Inc.

Piaget, J. e Inhelder, B.(1978a). Las operaciones intelectuales y su desarrollo. En J. Delval

(Ed), Lecturas en Psicología del Niño I (70-119) Edit. Alianza, Madrid.

Piaget, J. y Szeminska A.(1996). Génesis del Número en el Niño. Edit. Guadalupe, Argentina.

ARTÍCULOS RELACIONADOS

• Propuesta para la ejecución de una política educativa que permite enfrentar un problema de carácter intercultural en el sistema escolar chileno. (III parte)
• El trastorno del déficit atencional, ante la diversidad. (Parte II)
• El Trastorno del déficit Atencional, ante la Diversidad. (Parte I)
• Literatura infantil y educación en valores ante la influencia de los medios de comunicación (Parte IV)
• Literatura infantil y educación en valores ante la influencia de los medios de comunicación (Parte III)
• Literatura infantil y educación en valores ante la influencia de los medios de comunicación (Parte II)
• Literatura infantil y educación en valores ante la influencia de los medios de comunicación (Parte I)
• El trastorno del déficit atencional, ante la diversidad. (Parte IV)
• El trastorno del déficit atencional, ante la diversidad. (Parte IV)

OTROS TEMAS

Encuesta