!-- Google tag (gtag.js) -->


Busca:   en:
Inicio > Revista

¿Cómo trabajar en el salón de clase cuando tenemos muchos alumnos y grupos? (parte I)

En general, cuando se construye conocimiento , hay momentos en los que es importante detenerse a observar lo que se ha hecho, quizás, esa observación concluye en la determinación de alguna regularidad, útil para hacer la construcción del pensamiento. El artículo tiene como objetivo ilustrar por medio de la construcción de un triángulo de conocimiento, como dar clases cuando se tienen más de 50 alumnos por grupo y varios grupos.

INTRODUCCIÓN
“…solamente en aprender definiciones y teoremas, para reconocer el momento de utilizarlos y aplicarlos… hacer matemáticas implica ocuparse de problemas. Sólo se hacen matemáticas cuando nos ocupamos de problemas, pero se olvida que resolver un problema es parte del trabajo; encontrar buenas preguntas es tan importante como encontrar soluciones. Una buena reproducción por el estudiante de actividad científica exigiría que intervenga, que formule, que pruebe, que construya modelos, lenguajes, conceptos, teorías, que intercambie con otros, que reconozca los que están conformes con la cultura, que tome lo que es útil,…Por supuesto, se trata de una simulación que no es la “verdadera” actividad científica, como tampoco el saber presentado de forma axiomática constituye el “verdadero saber”” (Brousseau, 1986).
 
Los programas de Matemáticas de la Escuela Nacional Preparatoria, que imparten la materia obligatoria y con carácter teórica, muestra cambios significativos en la estructura, secuencia de los contenidos y en su enfoque metodológico, basado en la solución de problemas y no en relación aplicaciones prácticas. Por medio de los contenidos propuestos, pretende que el alumno conozca, comprenda y aplique el aprendizaje de una forma tradicional como lo marca la etapa de la educación de tecnología de la educación y no el constructivismo que marca las propuestas institucionales.
 
METODOLOGÍA
En la secuencia de la enseñanza de probabilidad elemental, hay una ruptura epistemológica: en la enseñanza elemental de estocásticos, los instrumentos simples de azar, como dados, juegos de barajas o ruletas, etc., se elaboran metódicamente de manera que parece que permiten una determinación inmediata de probabilidades y de posibilidades de combinación. Esta simplicidad inicial rápidamente reditúa una nueva dificultad: con la separación inicial de símbolos y modelos de las situaciones aleatorias concretas respectivas, los medios estocásticos ya no permiten encontrar soluciones directas y significados estocásticos. 
Steinbring (p.9)
 
Steinbring (1991) propone un triángulo relacional para explicar la naturaleza epistemológica de la apropiación de un concepto. Con el triángulo epistemológico (véase la Figura 1) se ilustra la interrelación entre sus componentes, de tal manera que no es posible deducir el significado de uno de los vértices sin considerar a los otros dos aspectos en una relación dialéctica que, conforme se estudian y desarrollan, posibilitan su enriquecimiento. La situación misma (el objeto) y el modelo estocástico (símbolo) no son suficientes para explicar los conceptos probabilísticos, sino que es necesaria la relación entre los tres para que el sujeto desarrolle la idea de azar y de probabilidad.
 
 
 
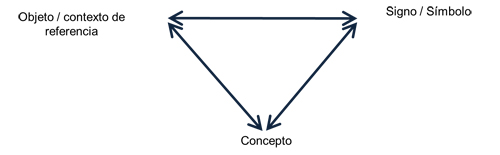
Figura 1. “El triángulo epistemológico representa un diagrama de relaciones en el que no se puede deducir el significado del conocimiento de uno de los vértices, el formal o el objeto” (Steinbring, 1989; en Steinbring, 1991, p. 6), sino que siempre se requiere de la interrelación de cada uno de los vértices del triángulo.
 
Este autor puntualiza que la constitución del conocimiento se basa en una perspectiva flexible donde las experiencias y los conceptos del estudiante están en continua relación.

 

Página siguiente
Gastos de envío
G R A T I S
Envíos España península para pedidos superiores a 59,90 euros (más iva) (condiciones)

Compartir en:

compartir FaceBook

Síguenos en: Síguenos en Twiter | Síguenos en Facebook | Instagram | pinterest

Enlaces rápidos a temas de interés

BOLETÍN

RSS | XHTML | CSS
Mapa Web | Registro | Contacta
© Majo Producciones 2001-2024 - Prohibida la reproducción parcial o total de la información mostrada